
ODD FREQUENCY
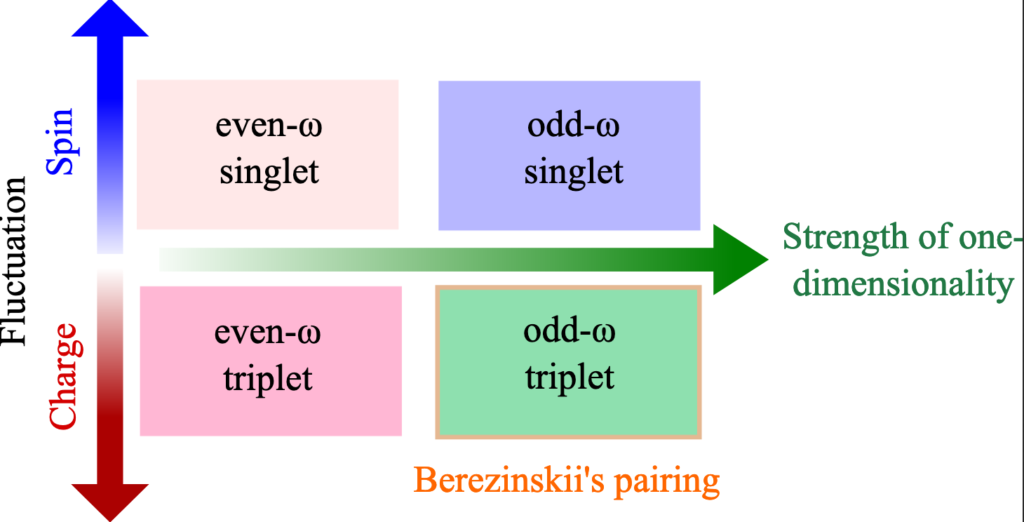
Odd frequency superconductivity (OFSC) or Berezinskii pairing is a nontrivial manifestation of dynamical order, where the Cooper pair amplitude is odd in relative time. This possibility extends the conventionally allowed symmetries of the pair amplitudes. It is a rich and testing playground for the dynamics of quantum matter.
MATERIAL INFORMATICS
Machine learning has entered the field of quantum matter with applications covering quantum materials and the many-body problem. Interpretable and computationally-efficient machine learning models are able to capture the structure-property relationship in materials science.
ODD-FREQUENCY
Organic Materials Database (OMDB)
Materials with competing ground states and phases constitute a challenge for ab initio based modeling. A prominent example are magnetic materials. We have extended the Organic Materials Database (OMDB) to include magnetic excitation properties.
DIRAC MATTER
Dirac matter can also be composed of bosons and not just fermions as it is normally assumed. If a large accumulation of bosons at the Dirac point is achieved, a Dirac BEC can be formed. The coherence is evident from Rabi oscillations between condensates on different sublattices.
Dirac materials
Dirac matter allows axial gauge fields sensitive to the nodal degree of freedom, corresponding to the motion of Weyl nodes in energy or momentum space. This effect can create a static magnetization via the dynamical axial electromagnetic fields in Dirac and Weyl semimetals.
Materials informatics
We developed a systematic approach to study magnetic phase diagrams that uses persistent homology, a recent computational method that is a type of topological data analysis. This method can capture both phases with and without long range magnetic order, such as the ferromagnetic and spin ice phase. Persistent homology also provides valuable insights into different phases.
Dark Matter Detection
Dirac materials have a wide range of applications and have even been proposed as a sensor material for dark matter particles. The energy range accessible by the small gap in massive Dirac cones provides the sensitivity to search in the sub-MeV mass scale. The small gap filters out the background thermal noise while still capturing excitations due to dark matter
PUMPED DIRAC MATTER
Driven or non-equilibrium Dirac materials offer a new platform for investigation of collective instabilities. Recent pump-probe photoemission experiments on graphene and three-dimensional (3D) topological insulators (TIs) show the existence of a long-lived population inversion, a situation when photoexcited electrons and holes form two independent Fermi-Dirac distributions. Motivated by these results, we propose to search for transient excitonic instability in optically-excited DMs with population inversion.
OPTICS - DIRAC MEDIA
The result of applying an external electromagnetic field on a medium manifests itself the creation of screening fields from within which consequently change the polarisation of the medium. The temporal dynamics of such polarisation fields then create electric currents. The relationship between the current and the external field is highly nontrivial in general, as it depends not only on the internal properties of the medium, but also on the excitation regime of the field. Low intensity fields tend to produce polarisations which scale linearly with the intensity and to generate currents oscillating at the same frequency as the external perturbation.
DIRAC AND WEYL SEMIMETALS
Dirac and Weyl semimetals are unique condensed matter materials, whose low-energy electron quasiparticles are described by the relativistic-like Dirac and Weyl equations, respectively. The hallmark properties of their quasiparticle states are their linear dispersion relations and well-defined chiralities. The band structure of Dirac and Weyl semimetals contains a discrete number of touching points known as the Dirac points and the Weyl nodes, respectively.
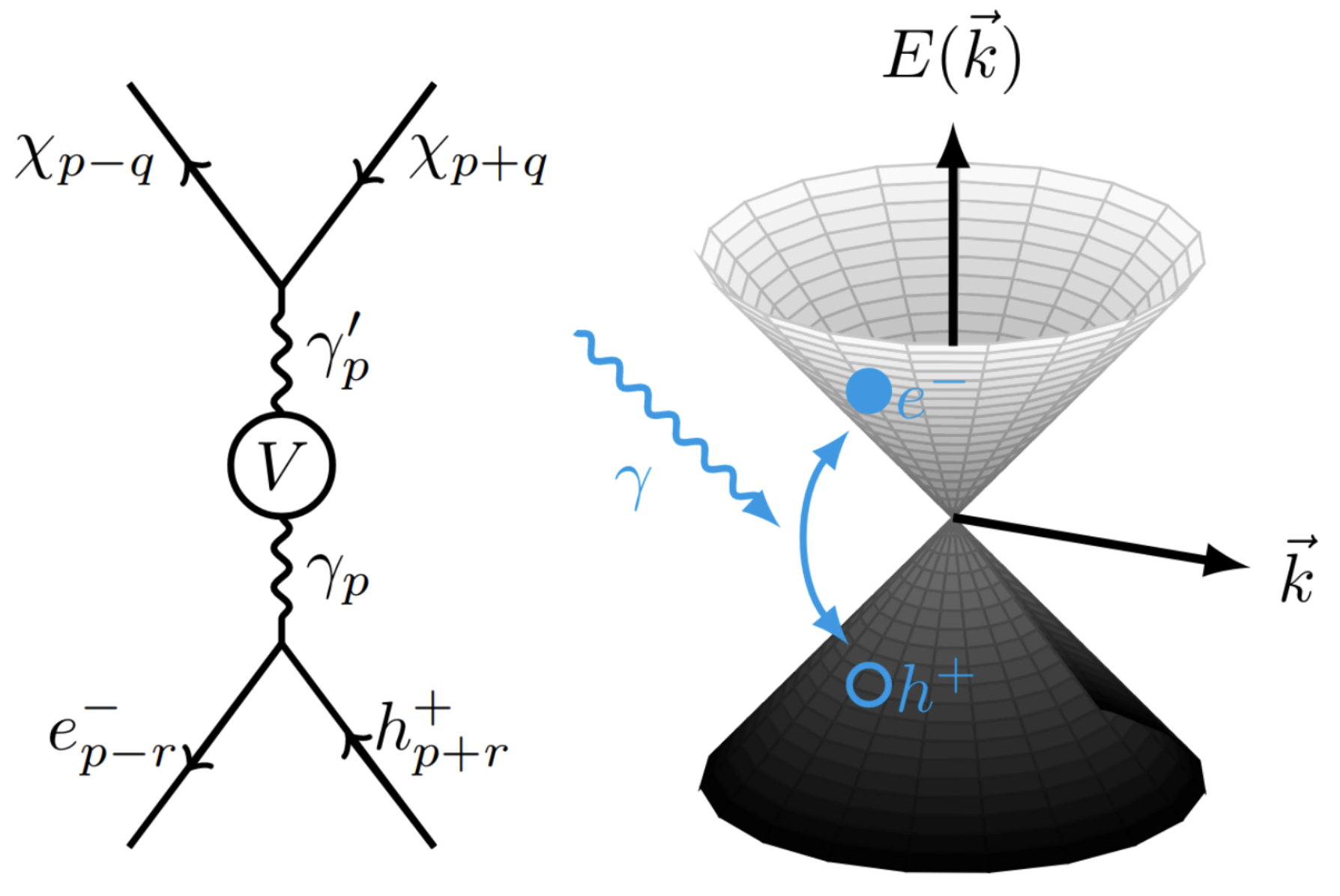
Odd-Frequency (Berezinskii) Pairing
Odd frequency superconductivity (OFSC) or Berezinskii pairing is a nontrivial manifestation of dynamical order, where the Cooper pair amplitude is odd in relative time. This possibility extends the conventionally allowed symmetries of the pair amplitudes. It is a rich and testing playground for the dynamics of quantum matter. Although bulk OFSC is yet to be identified, there are several proposals to realize such a system inmheterostructures, with broken translational symmetry, in a driven system with multiband superconductivity. Our group is currently working in several directions to identify the signatures of OFSC in the vicinity of paramagnetic impurities, Dirac semimetals, non-hermitian systems, amongst other candidate setups.
References :
[1] J. Linder, Jacob, A. V. Balatsky “Odd-frequency superconductivity.” (Review) (2017).

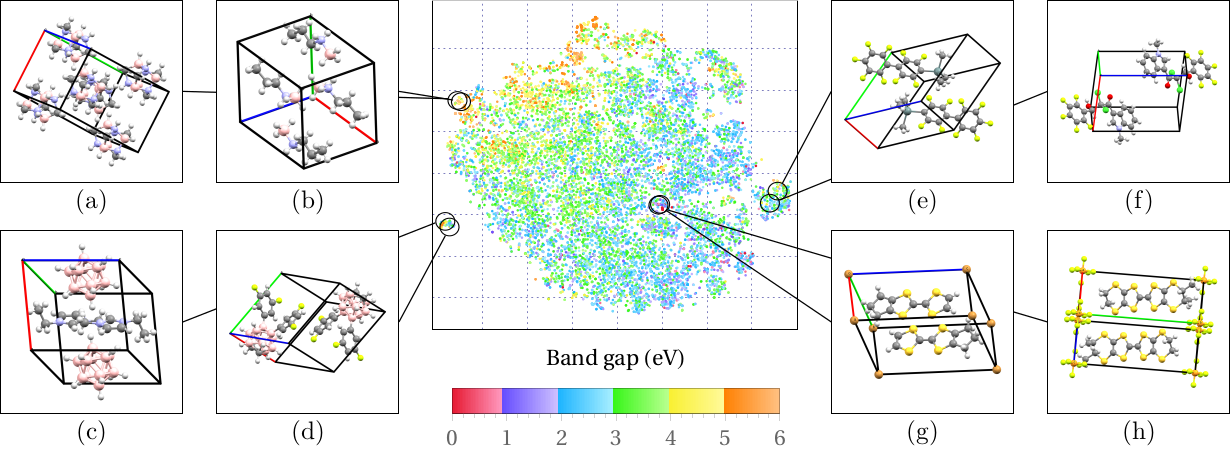
Machine learning for large organic crystal structures
Machine learning has entered the field of quantum matter with applications covering quantum materials and the many-body problem. Interpretable and computationally-efficient machine learning models are able to capture the structure-property relationship in materials science.
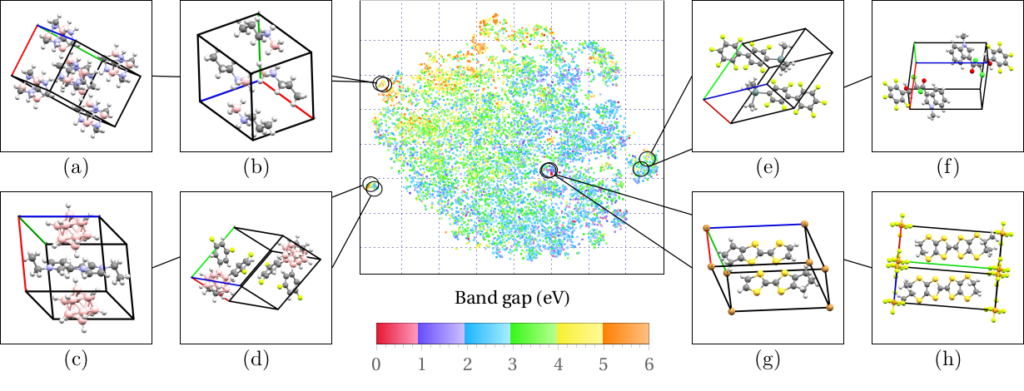
Among others, we use the organic materials database developed within our group as a training set for our machine learning studies. The database hosts electronic and magnetic structures of about 25,000 3-dimensional organic crystals and provides a highly complex dataset to work on. Applying machine learning we intend to provide predictions towards novel functional materials based on the properties calculated within our training sets.
References :
[1] B. Olsthoorn, R. M. Geilhufe, S. S. Borysov, A. V. Balatsky, Advanced Quantum Technologies, 2(7-8):1900023 (2019)
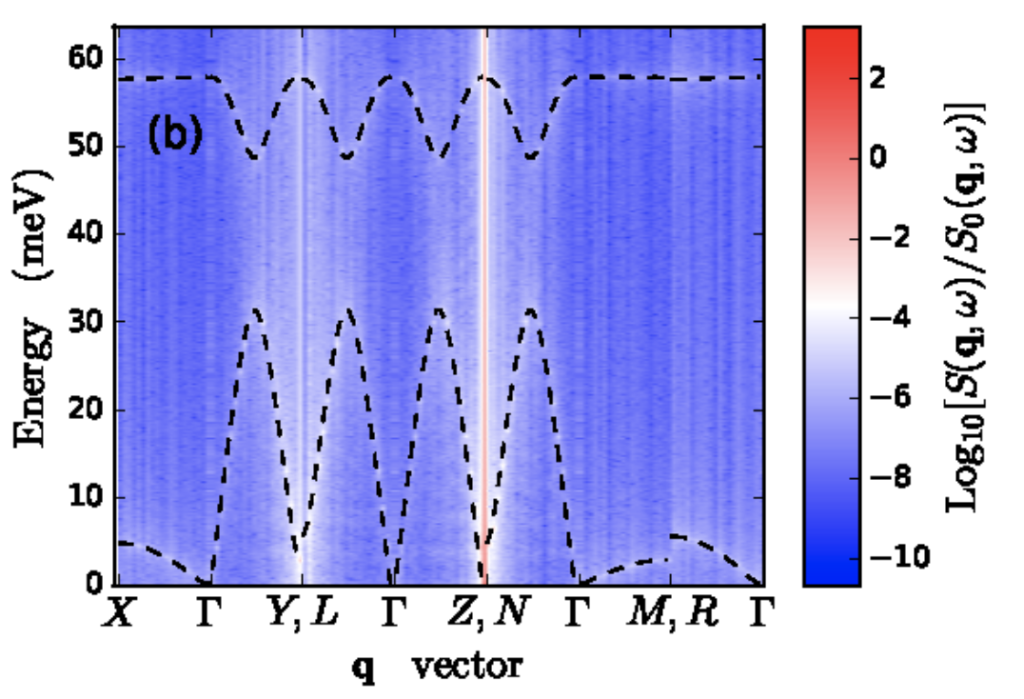
Magnetic excitations spectra on the Organic Materials Database (OMDB)
Materials with competing ground states and phases constitute a challenge for ab initio based modeling. A prominent example are magnetic materials. We have extended the Organic Materials Database (OMDB) [1] to include magnetic excitation properties. For inelastic neutron scattering we focus on the dynamical structure factor S(Q,ω) which contains information on the excitation modes of the material. The starting point is to consider magnetic materials within the OMDB. Using a ferromagnetic reference spin configuration, the magnetic Hamiltonian are obtained by using the infinitesimal rotation technique for calculation of Heisenberg exchange interactions.
For these magnetic Hamiltonians, quenching simulations down to zero temperature are performed in order to obtain the magnetic ground states. The magnetic excitation spectra are calculated by means of linear spin wave theory and atomistic spin dynamics simulations. The current dataset features collinear as well as noncollinear magnetic materials and has now been released on the OMDB. Representative results and the use of pattern matching algorithms to identify materials with desired properties are highlighted in [2].

References :
[1] S. S. Borysov, R. M. Geilhufe, and A. V. Balatsky, PLOS ONE 12, e0171501 (2017).
[2] J. Hellsvik, R. Díaz Pérez, R. M. Geilhufe, M. Månsson, and A. V. Balatsky, (2019).
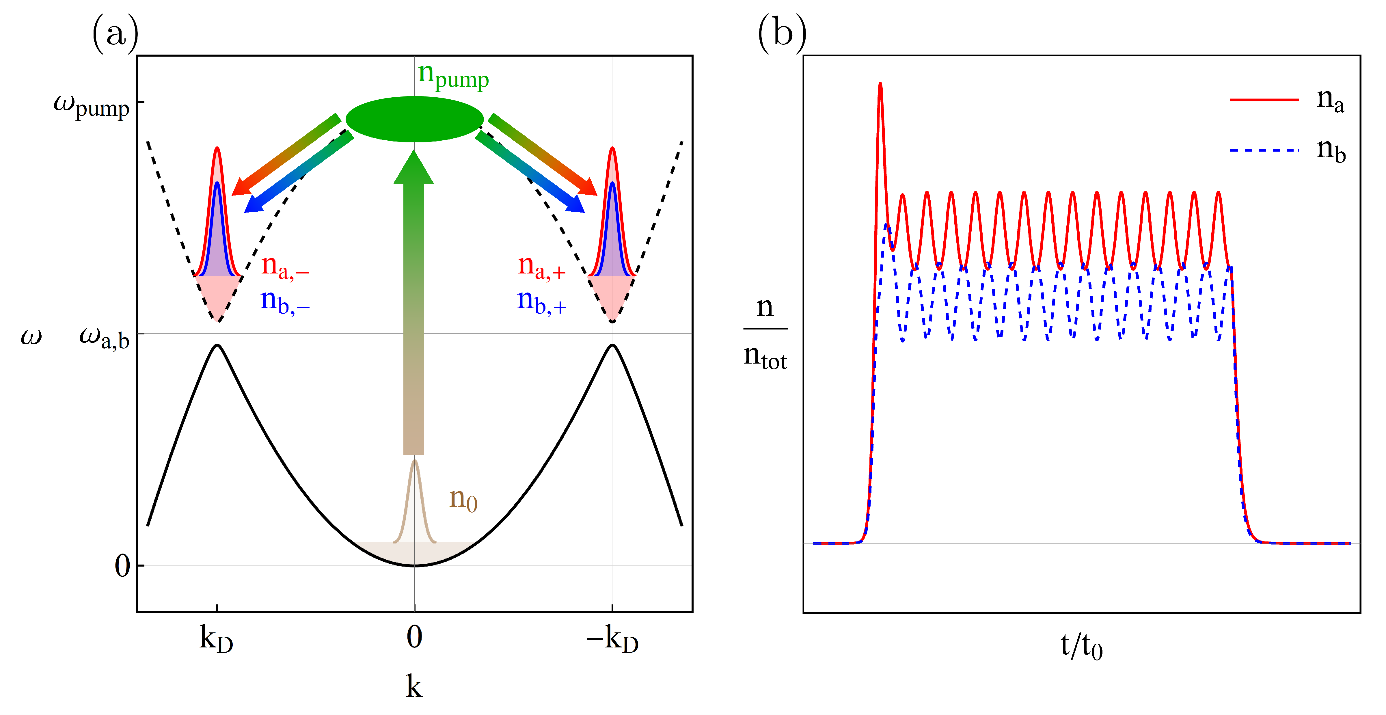
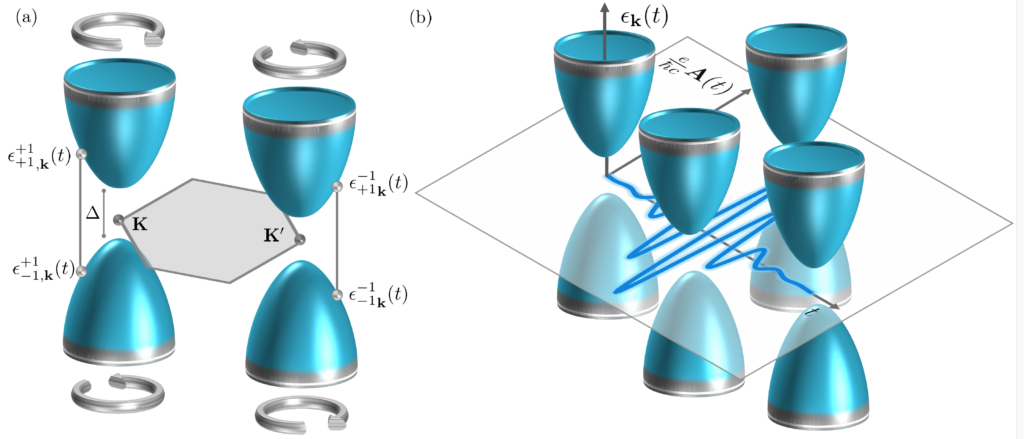
BosE-Einstein Condensate of Dirac Magnons
Discrete parity and time-reversal symmetries as well as non-Bravais lattices lead to the relativistic-like Dirac energy spectrum in both fermionic and bosonic Dirac materials. Recent studies show that 2D magnets such as transition metal trihalides CrI3 and CrBr3 realize a magnonic analog of graphene with a characteristic linear spin-wave spectrum in the vicinity of the Dirac nodes. However, unlike electron quasiparticles, no Pauli principle exists for bosons. Therefore, it is possible to create a significant occupation in the state with the same energy and, eventually, realize a Bose-Einstein condensate (BEC). Dirac nodes in the magnon spectrum, however, are located at higher energies where no magnons exist in equilibrium. Motivated by recent studies for conventional magnets such as yttrium-iron-garnet (YIG), we propose to create a steady-state nonequilibrium population at the Dirac nodes via pumping and realize the BEC of Dirac magnons (see panel (a) in the figure).
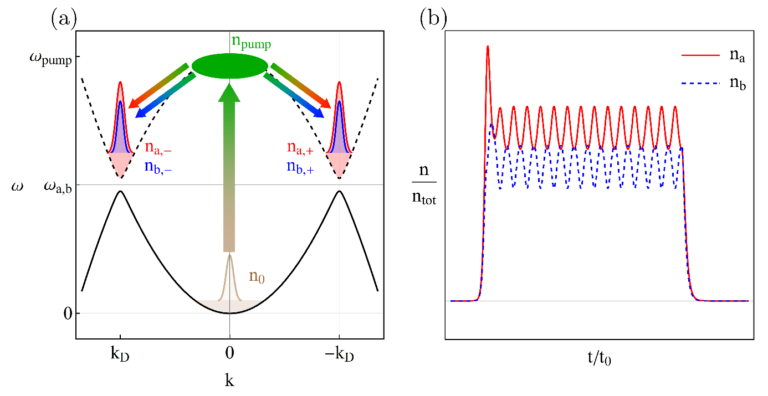
By using a phenomenological model of coupled Gross-Pitaevskii equations, we investigate the time evolution of the pumped condensate and the properties of collective modes. The multicomponent nature of the Dirac BEC is manifested in the Rabi oscillations between the populations with opposite pseudospins (see panel (b) in the figure). Depending on the ground state, the spectrum of collective modes contains either two gapless (Goldstone) or one gapped (Higgs) and one gapless collective modes of coherent Dirac BEC. The Haldane gap in the spectrum provides an efficient means to tune between the gapped and gapless collective modes as well as controls their stability.
References :
[1] S. S. Pershoguba, S Banerjee, J.C. Lashley, J Park, H. Ågren, G. Aeppli, A. V. Balatsky, Physical Review X 8 (1), 011010 (2018)
[2] P.O. Sukhachov, S. Banerjee, A.V. Balatsky, Physical Review Research 3, 013002 (2021)
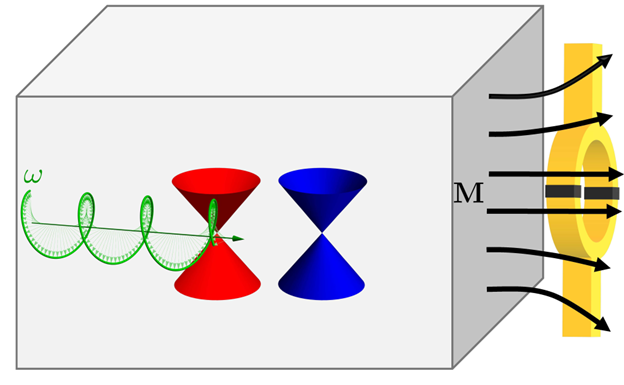
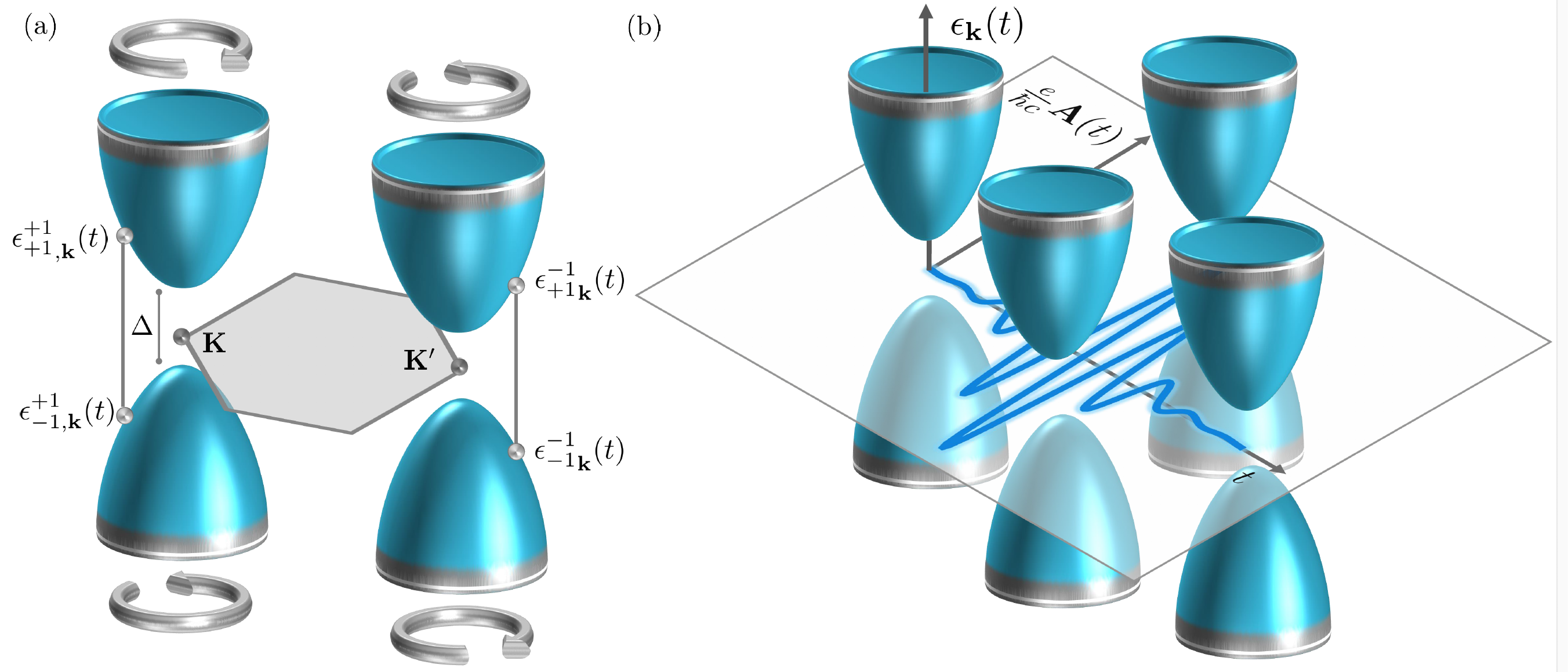
Axial Magnetoelectric Effect in Dirac Semimetals
The dynamics of excitations in quantum matter and their interplay with electromagnetic fields is a rapidly developing research area. We now witness the surge of interest in quantum matter with the unusual relativistic-like dispersion relation, namely Dirac materials. The relativistic-like energy spectrum and nontrivial topology of Dirac matter allow us to go beyond the conventional light-matter interaction paradigm and realize axial gauge fields sensitive to the nodal degree of freedom. These fields correspond to the motion of Weyl nodes in momentum or energy space and, for example, could be induced by dynamical strains. We propose a novel mechanism to generate a static magnetization via the dynamical axial electromagnetic fields in Dirac and Weyl semimetals (see figure for a schematic setup). This axial magnetoelectric effect (AMEE) originates from the transfer of the angular momentum of axial electric fields into the magnetic moment.

By using the realistic model parameters for the typical Dirac semimetal Cd3As2 and dynamical strains as a source of axial gauge fields, we estimate the induced magnetization to be observable by modern magnetometry. Our results uncover an unexplored correlation between dynamics of topological excitations and magnetization in Dirac materials as well as provide a way to investigate unusual axial electromagnetic fields via conventional magnetometry techniques.
References :
[1] Long Liang, P. O. Sukhachov, and A. V. Balatsky, arXiv: 2012.07888.
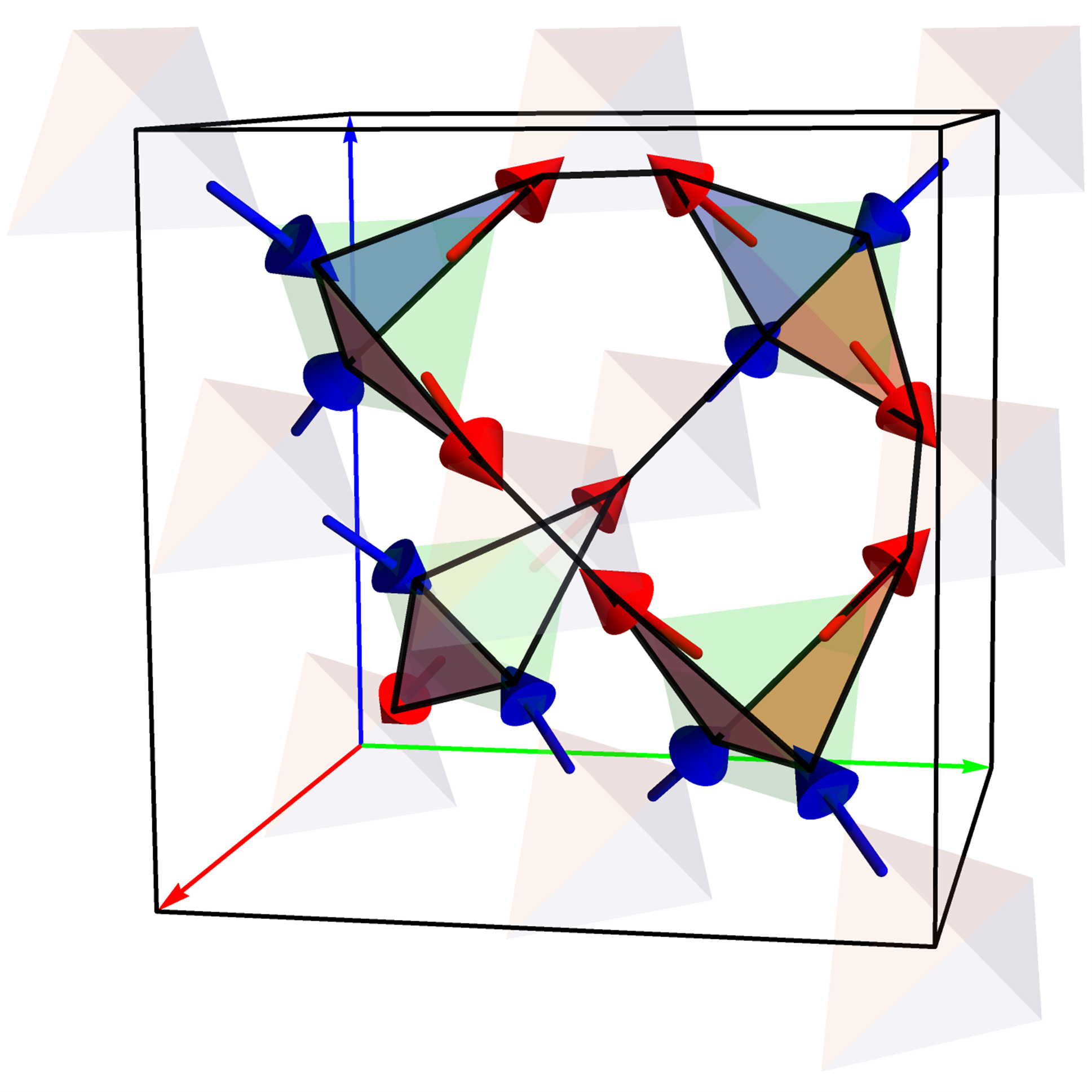
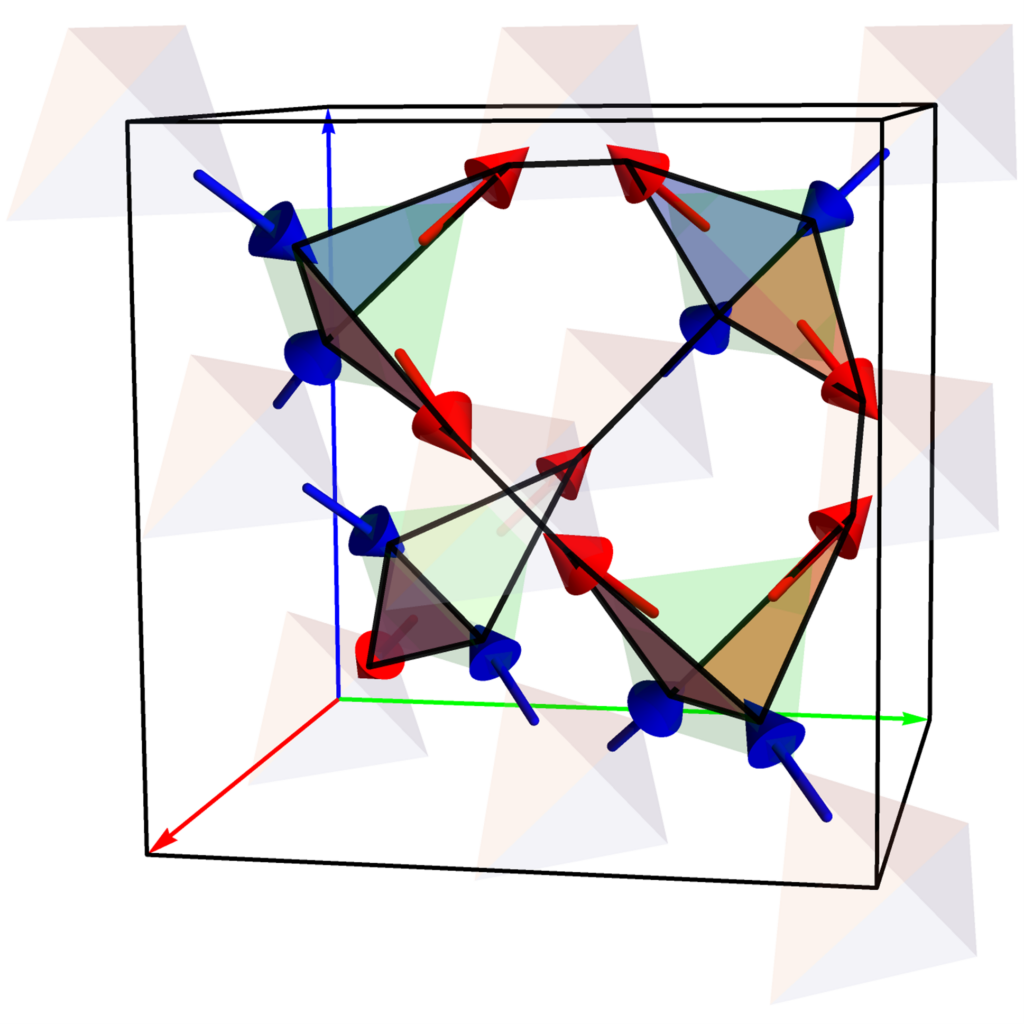
Persistent Homology for Magnetism
The rich phase diagram of spin models can contain many different phases, particularly in the presence of frustration between spins. Detecting and characterizing these phases by hand is a difficult task, and requires the construction of new order parameters. We developed a systematic approach that uses persistent homology, a recent computational method that is a type of topological data analysis. This method can capture both phases with and without long range magnetic order, such as the ferromagnetic and spin ice phase. In other words, a single method captures all phases rather than developing a distinct order parameter for each one. At the same time, persistent homology provides insight into each phase by revealing the characteristic length scales involved. The code involved in this demonstration has been open-sourced to the community and is available on Github.
References :
[1] B. Olsthoorn, J. Hellsvik, A. V. Balatsky, Phys. Rev. Research 2, 043308 (2020)
Dark Matter Detection
Dirac materials have a wide range of applications and have even been proposed as a sensor material for dark matter particles. The energy range accessible by the small gap in massive Dirac cones provides the sensitivity to search in the sub-MeV mass scale. The small gap filters out the background thermal noise while still capturing excitations due to dark matter. Moreover, an anisotropic Dirac cone should show daily modulation of the dark matter signal due to the Earth’s rotation.
In our group, we have applied Materials Informatics in the search for new candidate sensor Dirac materials. We have identified the first organic candidate material, the Dirac-line semimetal (BEDT-TTF)⋅Br, with a small gap of 50 meV. Additionally, we have studied the role of impurities in the sensor and their effect on Dark matter detection.
References :
[1] R. M. Geilhufe, B. Olsthoorn, A. D. Ferella, T. Koski, F. Kahlhoefer, J. Conrad, A. V. Balatsky, Physica Status Solidi Rapid Research Letters, Vol 12, 11 (2018)
[2] B. Olsthoorn, A. V. Balatsky (submitted) (2019)
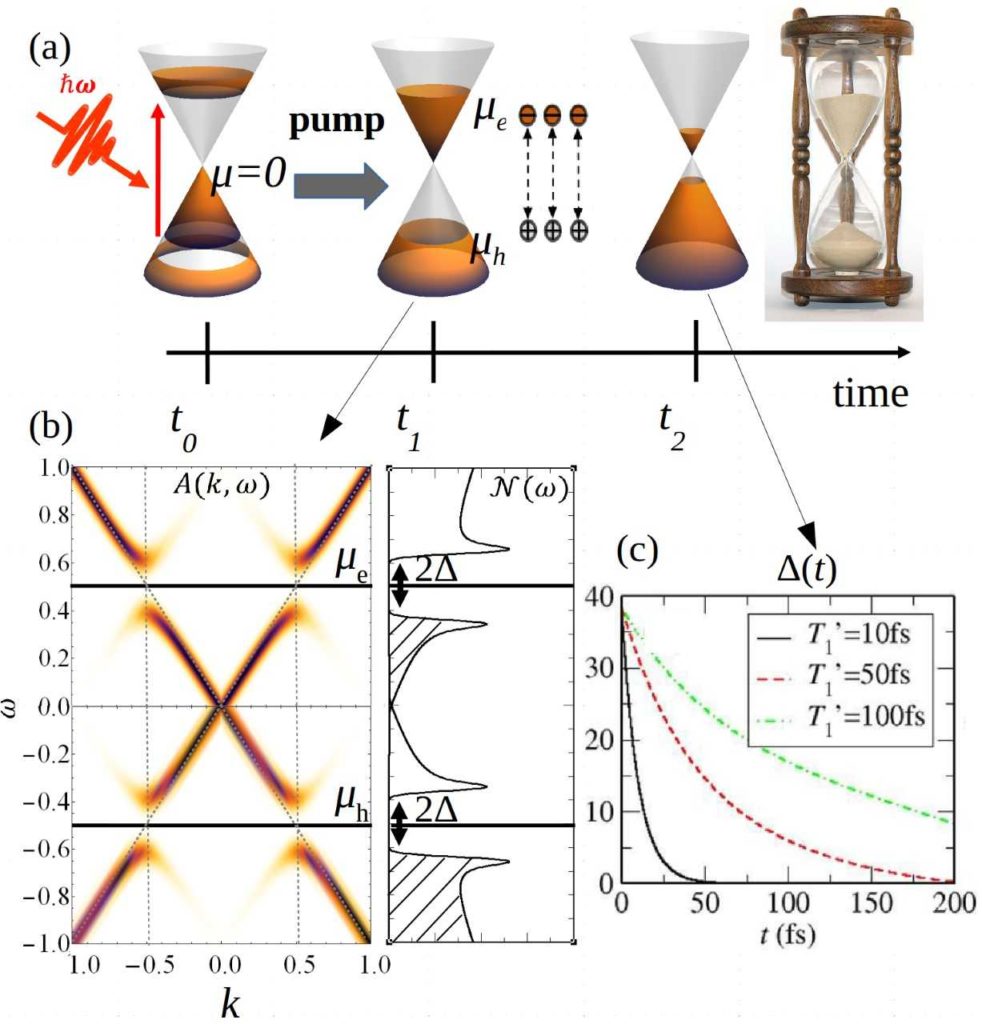
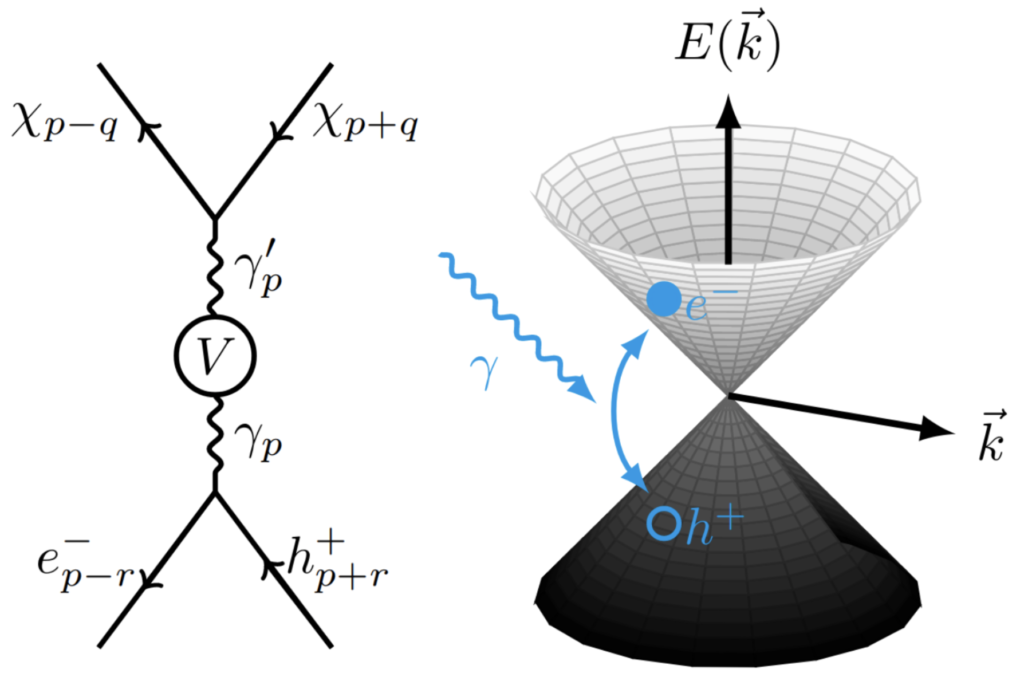
Transient excitonic condensate in pumped Dirac materials
Driven or non-equilibrium Dirac materials offer a new platform for investigation of collective instabilities. Recent pump-probe photoemission experiments on graphene and three-dimensional (3D) topological insulators (TIs) show the existence of a long-lived population inversion, a situation when photoexcited electrons and holes form two independent Fermi-Dirac distributions. Motivated by these results, we propose to search for transient excitonic instability in optically-excited DMs with population inversion. Optical pumping combined with the Dirac nature of the spectrum offers a knob for tuning the effective interaction between the photoexcited electrons and holes, and thus provides a way of reducing the critical coupling for excitonic instability. As a result, a transient condensate of electron-hole pairs could be achieved in a pumped DM while it is not attainable in equilibrium.
The key signature of the transient excitonic condensate are the energy gaps that open up at the non-equilibrium chemical potentials for electrons and holes, with the size of the gaps decreasing as the system returns to equilibrium (Fig.1). Among the existing DMs, the most promising candidates are (i) undoped suspended graphene, with gaps on the order of 10meV and a critical temperature of 70K, and (ii) 3D TIs with a single Dirac cone, where gaps of the order of few eV and critical temperatures of tens of K can be achieved. 3D TIs are particularly attractive due to prolonged lifetime of the population inversion. By tuning the material properties, it is possible to find new promising systems among 2D and 3D DMs.
References :
[1] C. Triola et al ,Phys. Rev. B 95, 205410 (2017)
[2] A. Pertsova and Balatsky, Phys. Rev. B 97, 075109 (2018)

Light-Matter interactions in Dirac materials
The result of applying an external electromagnetic field on a medium manifests itself the creation of screening fields from within which consequently change the polarisation of the medium. The temporal dynamics of such polarisation fields then create electric currents. The relationship between the current and the external field is highly nontrivial in general, as it depends not only on the internal properties of the medium, but also on the excitation regime of the field. Low intensity fields tend to produce polarisations which scale linearly with the intensity and to generate currents oscillating at the same frequency as the external perturbation. Depending on the bond strength and intrinsic lattice symmetries, certain optical features may be enhanced or suppressed. If the field strength is increased and resonant with some characteristic internal frequency, the system responds non-linearly and creates currents with a nontrivial harmonic composition. This has obvious technological applications in the development of optoelectronic devices and sensors.
Dirac materials have unusual optical properties. For instance, graphene does not have a direct band gap between its two optically-active bands and can therefore show resonant behaviour when excited with any frequency, making it highly transparent in the monolayer setup. It also shows universal conductivity in the low field regime, independent of any system parameters. Besides, it is a strong source of third-harmonics.
In our group, we work on understanding features of novel interactions in Dirac and Weyl semimetals and the role of the carrier features in optical observables such as currents or time-dependent carrier densities.
References :
[1] D. N. Carvalho, F. Biancalana, A. Marini Physical Review B, 97 (19), 195123. (2018)
[2] H. Rostami, M. Polini, Physical Review B 93.16, 161411. (2016)
Electronic properties of Dirac and Weyl semimetals
Dirac and Weyl semimetals are unique condensed matter materials, whose low-energy electron quasiparticles are described by the relativistic-like Dirac and Weyl equations, respectively. The hallmark properties of their quasiparticle states are their linear dispersion relations and well-defined chiralities. The band structure of Dirac and Weyl semimetals contains a discrete number of touching points known as the Dirac points and the Weyl nodes, respectively. Each Dirac point is doubly degenerate and consists of two overlapping Weyl nodes of opposite chirality. On the other hand, the degeneracy is lifted in Weyl semimetals whose nodes of opposite chirality are separated in momentum and/ or energy. Dirac and Weyl semimetals allow one to probe various quantum field effects in controlled conditions. Among them, the effects related to the chiral anomaly are among the most well-studied.
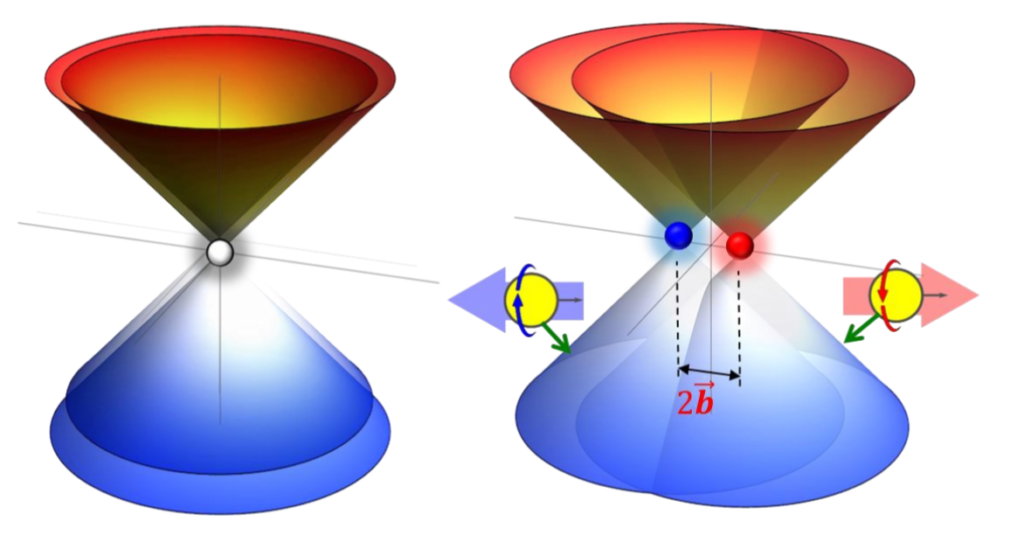
Furthermore, Dirac and Weyl semimetals demonstrate a vibrant variety of exotic phenomena on their own. Many of them are strongly affected by non trivial topology of Dirac and Weyl semimetals. In particular, the unusual properties include topologically protected surface Fermi arc states, unconventional charge and heat transport, strain-induced pseudo-electromagnetic (axial) gauge fields, new types of collective modes, unusual superconductivity, etc.
References :
[1] E. V. Gorbar, V. A. Miransky, I. A. Shovkovy, and P. O. Sukhachov, “Electronic Properties of Dirac and Weyl semimetals” (World Scientific, 2021)
[2] T. O. Wehling, A.M. Black-Schaffer, and A.V. Balatsky, Adv. Phys. 76, 1 (2014)

